J. Mol1*, P. M. Bayle1, M. Duran-Matute2, T. S. van den Bremer1
1 Delft University of Technology, The Netherlands; 2 Eindhoven University of Technology, the Netherlands
* Corresponding author: j.mol@tudelft.nl
Introduction
Understanding particle transport in the ocean is crucial for predicting the distribution of nutrients (Gruber et al. 2011), plankton (Nooteboom et al. 2019) and pollutants including plastic litter (van Sebille et al. 2020) as well as for search-and-rescue operations (Breivik et al. 2013). Particle transport is influenced by processes over a wide range of scales, from large-scale ocean gyres to small-scale turbulent mixing (Sutherland et al. 2023). One of the important processes for particles floating on or suspended near the ocean surface is transport due to surface gravity waves. Such particles experience a net drift in the wave direction known as Stokes drift (Stokes 1847). When the Earth's rotation is accounted for, waves induce an additional (Eulerian-mean) current that reduces drift and is known as the anti-Stokes drift. This effect is often ignored in oceanic particle-tracking simulations, despite being important. Although different theoretical models exist, they have not been validated by experiments.
Objective and Methods
We conduct laboratory experiments studying the surface drift induced by deep-water waves in a purpose-built rotating wave flume. The wave flume is 2.2 m long, 0.5 m wide with a water depth of 0.15 m and is placed on top of a rotating table with a diameter of 1.7 m. The position of 2 mm floating spherical particles is recorded with a downward-looking camera.
The experimental results are compared to three existing theoretical models with different assumptions. In what we term the forced-steady model (Weber 1983), a wind stress (normal to the surface) exactly compensates the viscous attenuation of the wave field and all time dependence is neglected. In what we term unforced models, no forcing is put in place to ensure that the wave field is of permanent form. The unforced-unsteady model (Madsen 1978) neglects all time dependence, while the unforced-unsteady model (Higgins et al. 2020) allows for variations on inertial time scales. At the surface these models only depend on the non-dimenational wave Ekman number Ek-1 = Ω/(4νk2), which determines the relative importance of rotation and viscosity.
Results
As a wave passes, the particle moves forward with the crest of the wave and backward with the trough. Averaging over this movement, we find a net drift. Without rotation, this drift is in the same direction as the waves, as expected from the Stokes drift. When the setup is rotating, the particles instead drift to the right of the wave direction (for counterclockwise rotation) while decribing inertial circles.
Averaging over the full trajectory of a particle, we find the mean drift speed (see Figure 1). Increasing the rotation rate reduces the magnitude of the mean drift speed. Compared to two existing steady theoretical models, measured drift speed follows a similar trend with wave Ekman number (Ek-1 = Ω/(4νk2) but is larger. The difference is largely explained by unsteadiness on inertial time scales, as shown by the improved agreement with the unforced-unsteady model. Our results emphasise the importance of considering unsteadiness when predicting and analysing the transport of floating material by waves.
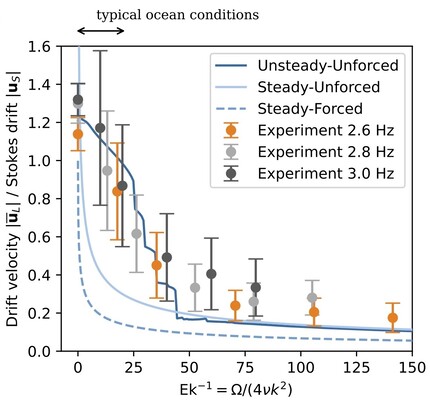
Figure 1. Comparison between experiments and theory for the average drift speed at the surface normalised by the predicted Stokes drift as a function of the wave Ekman number Ek^-1.
References
Breivik, Ø., Allen, A. A., Maisondieu, C., & Olagnon, M. (2013). Advances in search and rescue at sea. Ocean Dynamics, 63 (1), 83–88.
Gruber, N., Lachkar, Z., Frenzel, H. et al. (2011). Eddy-induced reduction of biological production in eastern boundary upwelling systems. Nature Geoscience, 4 (11), 787–792.
Higgins, C., Vanneste, J., & van den Bremer, T. S. (2020). Unsteady Ekman-Stokes dynamics: Implications for surface wave-induced drift of floating marine litter. Geophysical Research Letters, 47 (18), e2020GL089189.451.
Madsen, O. S. (1978). Mass transport in deep-water waves. Journal of Physical Oceanography, 8 (6), 1009 – 1015.
Nooteboom, P. D., Bijl, P. K., van Sebille, E., von der Heydt, A. S., & Dijkstra, H. A. (2019). Transport bias by ocean currents in sedimentary microplankton assemblages: Implications for paleoceanographic reconstructions. Paleoceanography and Paleoclimatology, 34 (7), 1178-1194.
Stokes, G. (1847). On the theory of oscillatory waves. Transactions of the Cambridge Philosophical Society, 8 , 441-445.
Sutherland, B. R., DiBenedetto, M., Kaminski, A., & van den Bremer, T. S. (2023). Fluid dynamics challenges in predicting plastic pollution transport in the ocean: A perspective. Physical Review Fluids, 8 , 070701.
van Sebille, E., Aliani, S., Law, K. L. et al. (2020). The physical oceanography of the transport of floating marine debris. Environmental Research Letters, 15 (2), 023003.
Weber, J. E. (1983). Steady wind- and wave-induced currents in the open ocean. Journal of Physical Oceanography, 13 (3), 524 – 530.










