M. Siemerink1,2*; N.D. Volp1,2; E.M. Horstman2; P.C. Roos2
1Nelen & Schuurmans; 2University of Twente
* Corresponding author: martijn.siemerink@nelen-schuurmans.nl
Introduction
Management and conservation of estuarine environments is often supported by hydrodynamic models to help assess impacts of management interventions. In such models, the simulation of detailed flow patterns is important for predicting future morphological and ecological developments. However, due to the spatial scales of estuaries, detailed hydrodynamic simulations are very time consuming. Subgrid-based hydrodynamic models reduce the computational cost for such large-scale hydrodynamic simulations. The subgrid-based method computes water levels and flow velocities at a coarse resolution grid, whereas high resolution input data is used to guarantee an accurate computation of wetting and drying, and effects of friction and advection. (Casulli, 2009; Volp et al., 2013). To obtain detailed flow patterns from the coarse grid results, a velocity reconstruction must be performed. In previous studies, an accurate flow velocity reconstruction has been achieved for uniform structured grids (Volp et al., 2016), but has never been applied to real-life estuaries with spatially varying computational grid sizes. This study aims to create a flow velocity field at high resolution for a non-uniform, structured computational grid that is applied to real-life estuarine environments.
Objective and Methods
Real-life applications of subgrid-based hydrodynamic models can benefit from a non-uniform, structured computational grid. For example, increasing the grid resolution in areas with high flow variability and in regions of interest. The presented flow velocity reconstruction uses the results of a subgrid-based hydrodynamic model. The computations are based on square computational cells, where a quadtree structure allows for different computational grid resolutions across the model domain. The quadtree structure allows for transitions between grid cell widths of a factor two (Stelling, 2012). The quadtree structure and square grid cells allow for an independent evaluation of flow velocity components in x- and y-direction. The flow velocity reconstruction consists of two stages: i) interpolating water levels from the computational grid to the subgrid, and ii) reconstructing flow velocity components in the x- and y-direction on the subgrid. To capture the basic physics the reconstruction is based on the continuity principle in streamwise direction and a simplified momentum balance in cross-stream direction (Volp et al., 2016).
Results
The presented flow velocity reconstruction method is applied to both theoretical testcases, and real-life examples. It will be shown that the method is accurate and applicable under real-life estuarine conditions. Consequently, we can demonstrate the potential it has for dealing with wetting and drying, and for allowing sediment transport computations with limited computational costs. This creates the possibility for more efficient long-term simulations suited to forecast morphological and ecological developments.
The theoretical testcase shows the detailed flow pattern in a bend with a crossflow gradient in the bathymetry. This testcase demonstrates the ability and accuracy of this new method to capture the distribution of flow velocities across the depth profile within a coarse grid cell. For a real-life example the method is applied to the Elbe estuary. The model will be set up using different computational grid resolutions with the quadtree structure across the domain (Korporaal, 2024). We expect the model results for this real-life situation to show a good ability to efficiently compute flow patterns at the fine grid resolution for a complex system such as the Elbe and to give insight in reducing computational cost with respect to traditional methods.
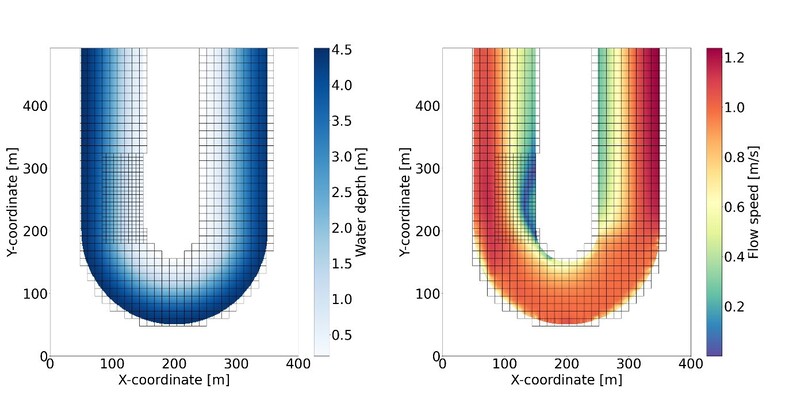
Results of the reconstruction steps for a simulation of a schematised bend with varying bathymetry (deep outer bend and shallow inner bend). Computations are based on a high resolution grid (subgrid) of 1m x 1m and a computational grid of 12m x 12m with a refined area of 6m x 6m. Left: Water depth based on the water level interpolation. Right: Reconstructed flow speed.
References
Casulli, V. (2009). A high-resolution wetting and drying algorithm for free-surface hydrodynamics. International Journal for Numerical Methods in Fluids, 60(4), 391–408. https://doi.org/10.1002/fld.1896
Korporaal, K. (2024). Structuring the hydrodynamics of the Elbe estuary. http://essay.utwente.nl/104129/
Stelling, G. S. (2012). Quadtree flood simulations with sub-grid digital elevation models. Proceedings of the Institution of Civil Engineers: Water Management, 165(10), 567–580. https://doi.org/10.1680/wama.12.00018
Volp, N. D., van Prooijen, B. C., Pietrzak, J. D., & Stelling, G. S. (2016). A subgrid based approach for morphodynamic modelling. Advances in Water Resources, 93, 105–117. https://doi.org/10.1016/j.advwatres.2015.07.013
Volp, N. D., Van Prooijen, B. C., & Stelling, G. S. (2013). A finite volume approach for shallow water flow accounting for high-resolution bathymetry and roughness data. Water Resources Research, 49(7), 4126–4135. https://doi.org/10.1002/wrcr.20324










