L. Portos-Amill1*, P.C. Roos1 , H.M. Schuttelaars2, S.J.M.H. Huslcher1
1 University of Twente, Netherlands; 2 Delft University of Technology, Netherlands
* Corresponding author: l.portosamill@utwente.nl
Introduction
Tidal sand waves are rhythmic bed features often found in tidally-dominated shelf seas. They have wavelengths of 100 - 1000m, heights of 1 - 10 m, and migration rates of 1 - 10 m/yr (van Dijk and Kleinhans, 2005).
Hulscher (1996) explained sand wave formation as a free instability of a flat seabed subject to tidal motion using a linear stability analysis. Recently, observations have indicated that the underlying topography affects the shape of a sand wave field, by yielding, e.g., more two-dimensional sand wave fields on top of sand banks than on the sandbank slopes (Krabbendam et al., 2023). However, the effects of a sloping shelf on sand wave formation have not been studied in detail.
We aim to systematically study the effects of a sloping background topography on the initial stage of sand wave growth. Similarly to the shoreface-connected sand ridges study of Calvete et al. (2001), we make use of a linear stability analysis.
Objective and Methods
Consider an offshore region of a shallow shelf sea with an alongshore-uniform background topography that is sloping in the cross-shore direction y, H(γy). We assume a weak cross-shore dependence, hence γ is small. The background topography is in morphodynamic equilibrium, on top of which sand waves may develop (Figure 1).
We build a model based on the 3D shallow water equations, where bed evolution is modelled with the Exner equation, considering bedload sediment transport. The model is forced with an M2 tidal signal in the alongshore direction. We assume periodicity in the alongshore direction.
We then perform a linear stability analysis on the model equations, which allows us to study the growth or decay of seabed perturbations on the basic state topography (the shelf without sand waves).
The weak dependence on y of the shelf topography allows for solving the basic state semi-analytically, by expanding the equations in terms of the small parameter γ. The first-order solution is characterised by a sinusoidal dependence on the alongshore coordinate, with wavenumber k. For each k-value, the stability analysis yields the mode (flow and bathymetry) with the highest growth rate, which is often considered to characterise the system.
Results
The basic flow shows tide-topography interactions leading to upslope residual currents at the seabed similar to those over sandbanks. These effects depend on both the local depth and slope.
Our first-order model reproduces the flow over an imposed hypothetical sand wave topography. It is also able to compute the fastest growing mode for the flatbed case, with γ = 0, reproducing the results of Hulscher (1996). Results on the stability analysis for a non-zero shelf slope (γ > 0) will be presented at the conference.
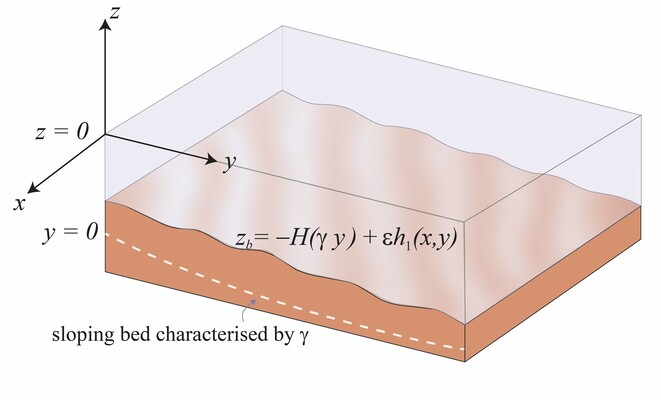
Figure 1: Sketch of the model geometry, with alongshore coordinate x, cross-shore coordinate y and vertical coordinate z.
References
Calvete, D., Falqués, A., De Swart, H. E., & Walgreen, M. (2001). Modelling the formation of shoreface-connected sand ridges on storm-dominated inner shelves. Journal of Fluid Mechanics, 441, 169-193.
Hulscher, S. J. (1996). Tidal‐induced large‐scale regular bed form patterns in a three‐dimensional shallow water model. Journal of geophysical research: Oceans, 101(C9), 20727-20744.
Krabbendam, J., Nnafie, A., Borsje, B., & de Swart, H. (2023). Background topography affects the degree of three‐dimensionality of tidal sand waves. Journal of Geophysical Research: Earth Surface, 128(11), e2023JF007153.
Van Dijk, T. A., & Kleinhans, M. G. (2005). Processes controlling the dynamics of compound sand waves in the North Sea, Netherlands. Journal of Geophysical Research: Earth Surface, 110(F4).


